Project Title
On The Extension Of The Polygamma Function To Non-Integer Order
Research Team
Contact Information
Fin. Omar Alsaid Sulaiman
External colaborator: Dr. Arran Fernandez
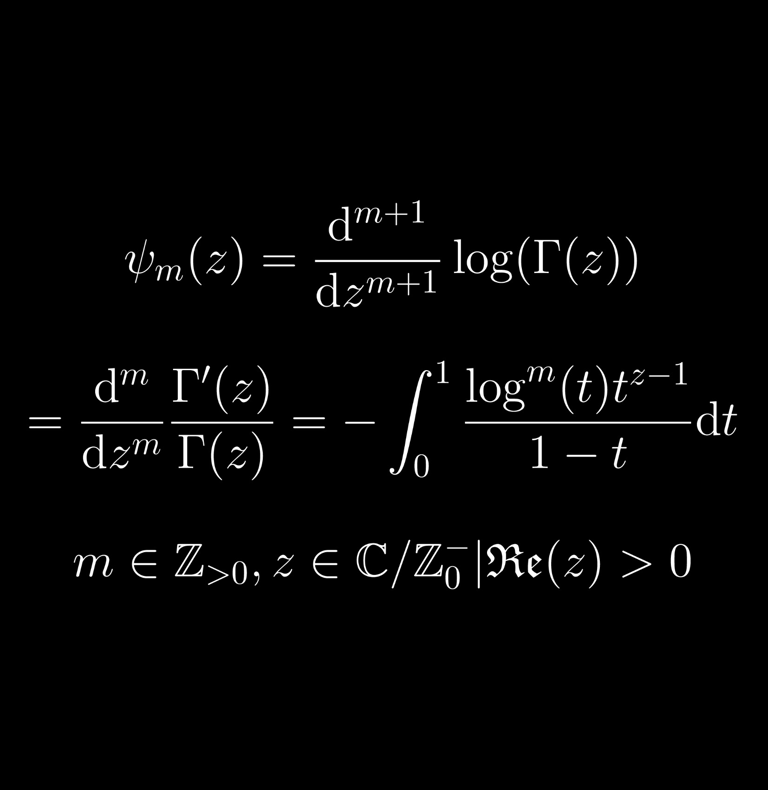
Institutional e-mail:
Overview
The polygamma function is a special function introduced as a generalization of the more well-known digamma function. It is defined, as a function of a single variable depending also on a non-negative integer parameter m, as the mth derivative of the digamma function, or equivalently the (m + 1)th derivative of the logarithm of the gamma function. It has several interesting properties and is an established part of the theory of special functions. In this paper, we investigate what happens when m is allowed to take non-integer values. This naturally involves using the theory of fractional calculus, which gives meaning to derivatives of non-integer order. One of the curiosities of fractional calculus is that there is no single unique way to define derivatives to non-integer order, but instead many competing definitions. After reviewing some of the most standard efinitions as well as some general classes of operators that include many different types of fractional calculus within a single framework, we will examine how these operators can be used to produce fractional versions of the polygamma function. There will of course be many different possible “fractional polygamma functions” according to which type of fractional derivative is used, and therefore the structure will be more rich and varied than that of classical polygamma functions.
Alternative e-mail:
omar.alsaid@czetesis.com
omar-alsaid-sulaiman@outlook.com
