Título del Proyecto

Extensión de la función poligamma a órdenes no enteros

Equipo de Investigación

Información de Contácto

Lic. Omar Alsaid Sulaiman

Colaborador Externo: Dr. Arran Fernandez

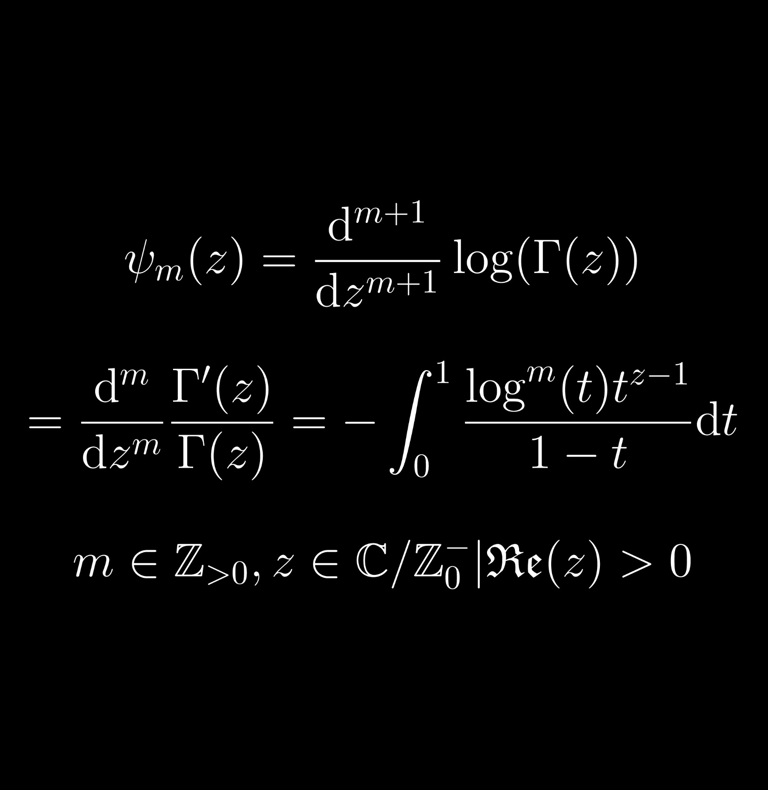
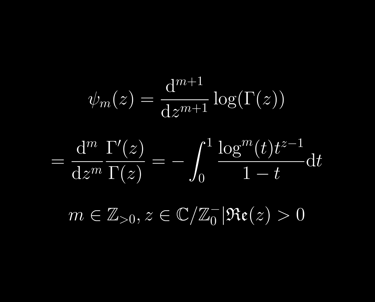
Correo institucional

Resumen

La función poligamma es una función especial introducida como generalización de la función digamma, más conocida. Se define, como una función de una sola variable que depende también de un parámetro entero no negativo m, como la m-ésima derivada de la función digamma, o equivalentemente la (m + 1) derivada del logaritmo de la función gamma. Tiene varias propiedades interesantes y forma parte de la teoría de funciones especiales. En este artículo investigamos qué ocurre cuando se permite que m tome valores no enteros. Esto implica, naturalmente, utilizar la teoría del cálculo fraccionario, que da sentido a las derivadas de orden no entero. Una de las curiosidades del cálculo fraccionario es que no existe una única manera de definir las derivadas de orden no entero, sino muchas definiciones que compiten entre sí. Después de revisar algunas de las definiciones más estándar, así como algunas clases generales de operadores que incluyen muchos tipos diferentes de cálculo fraccionario dentro de un único marco, examinaremos cómo pueden utilizarse estos operadores para producir versiones fraccionarias de la función poligamma. Por supuesto, habrá muchas «funciones poligamma fraccionarias» posibles según el tipo de derivada fraccionaria que se utilice y, por lo tanto, la estructura será más rica y variada que la de las funciones poligamma clásicas.

Correo alternativo

omar.alsaid@czetesis.com

omar-alsaid-sulaiman@outlook.com